Simple trick for remembering where the standard trigonometric angles are

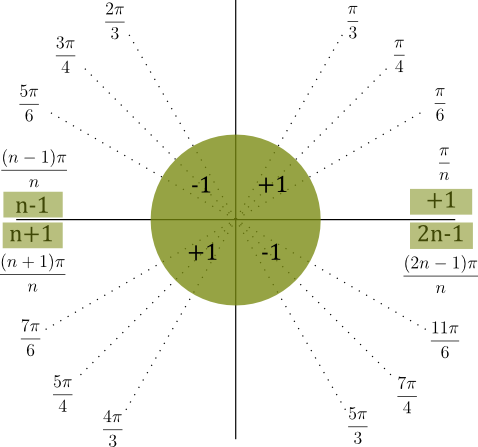
If you have difficulty remembering where the standard angles are, there is a simple way to do so.

First, remember that we are talking about the /6, /4, and /3 angles only.  The /2 angles (0, π/2, π, and 3π/2) don’t fit into this method very well, and other angles (eg π/12, 5π/12) don’t work at all.

Second, note that there is only one of each of the /6, /4, and /3 angles in each quadrant. 

Third, there is a pattern that each of the quadrants follows based on the angle you are trying to locate.  Quadrant I is easiest – it is always just π over the denominator.  For example, Quadrant I has π/6, π/4, and π/3.  Quadrant II has a numerator one less than the denominator, 2π/3, 3π/4, and 5π/6.  Quadrant III has a numerator one more than the denominator, 7π/6, 5π/4, and 4π/3.  Quadrant IV has one less than twice the denominator, 5π/3, 7π/4, and 11π/6.  So for Quadrants I, II, III, and IV, the pattern is +1, –1, +1, –1.  This is summarized in the following chart:

Trig Identities Memory Aid

Here’s a handy memory aid if you need help remembering the trig identities. 

The chart is composed of each of the basic 6 trig functions arranged on a circle.  The position of each function is important, so make sure you remember that.  To assist, it is helpful to note that all of the co-functions are on the right, and each one is the co-function of the normal function directly on its left.  Then you only have to remember that the order of the functions on the left is sin, tan, sec.  Some of the functions are connected in a triangular pattern that represents the basic trigonometric pythagorean identities.

There are three important identities that are represented in this chart, summarized below the image.

Diagonals are reciprocals

On the circle, functions that are directly across from each other are reciprocals.  Thus, sin=1/csc , cos=1/sec, cot=1/tan, csc=1/sin, sec=1/cos, and tan=1/cot.  Easy. 

For each triangle, a² + b² = c²

There are three triangles identified on the diagram.  For each one, you can obtain the Pythagorean identities by filling in the a, b, and c appropriate.  Note that a, b, and c are always in the same position on the triangle (upper left, upper right, and bottom).

sin2 + cos2 = 12 tan2 + 12 = sec2 12 + cot2 = csc2

sin2 + cos2 = 1 tan2 + 1 = sec2 1 + cot2 = csc2

Around the circle, each function is the product of the two functions next to it

Any function on the circle is the product of the two functions on either side of it.  Thus:

sin = tan ∙ cos
cos = sin ∙ cot
cot = cos ∙ csc
csc = cot ∙ sec
sec = csc ∙ tan
tan = sec ∙ sin

Because of rule #1, you could also say that the rule applies diagonally as well.  So:

sin ∙ csc = 1
tan ∙ cot = 1
sec ∙ cos = 1